导数
\[ f'(x)=\frac{d y}{d x}=\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x} \]
- \(\,\ \, \,\) 问题: 求导数与用导数
- 求导数: 用定义, 用运算法则.
- 用导数: 几何意义, 微分中值定理, 泰勒公式
1 导数是什么
- 主要问题是求导数和用导数.
\[ f'(x)=\frac{d y}{d x}=\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}. \]
- 微商: 微分的商, 分子分母\(dy ,dx\) 可以单独计算
- 可导必连续, 连续不一定可导.
导数如果存在, 则表示切线的斜率.
注意唯一的一种情况: 切线存在不一定可导(导数是无穷大).
2 求导数
一点处的导数用定义求
用运算法则求导数.
注意函数有不同的表达方式, 对应有相应的求导法则. 但归根结底就一条: 导数是微商.
高阶导数是导数的导数, 和导数没什么不同. 需要注意的是记号.
\[ f'(x)=\frac{d y}{d x}=\lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}. \]
分段函数的分界点用定义计算.
左右导数.
2.1 导函数用运算法则
\[\begin{align} (u\pm v)'=u'\pm v',\\ (uv)'=u'v+uv',\\ (\frac{u}{v})'=\frac{u'v-uv'}{v^2}.\\ \end{align} \]
设\(y=f(u), u=g(x).\)则 \[ y'=f'(u)g'(x). \] 写成微分的形式: \[ \frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}. \]
设 \[ \left\{\begin{align} x=\varphi(t)\\ y=\psi(t) \end{align} \right., 则 \] \[ \frac{d y}{d x}=\frac{d \psi(t) }{d \varphi(t) }=\frac{\psi'(t) }{\varphi'(t)}. \]
用微分计算.
注意分子分母不要混淆.
设\(F(x, y)=0\), 两边分别是对\(x\)求导即得.
也可两边求微分得.
3 微分及运算法则
- 计算 \[ d y=f'(x)d x. \]
- 可微等于可导.
和导数的法则对应.
四则运算 \[\begin{align} d(u\pm v)=du\pm dv,\\ d(uv)=vdu+udv,\\ d(\frac{u}{v})=\frac{vdu-udv}{v^2}.\\ \end{align} \]
复合函数(即一阶微分形式不变性) \[ df(u)=f'(u)du=f'(u)g'(x)dx. \]
求微分时, 不管变量\(u\)是一个字母还是一个表达式, 都可以看成一个整体\(u\).
求微分就是用符号\(d\) 一下, 然后用运算法则求下去就行.
\[ \Delta y\approx d y,\quad \Delta y-d y= o(\Delta x). \]
微分可以作为\(\Delta y\)的近似值, 误差是\(\Delta x\)的高阶无穷小.
以直(\(d y\))代曲(\(\Delta y\)).
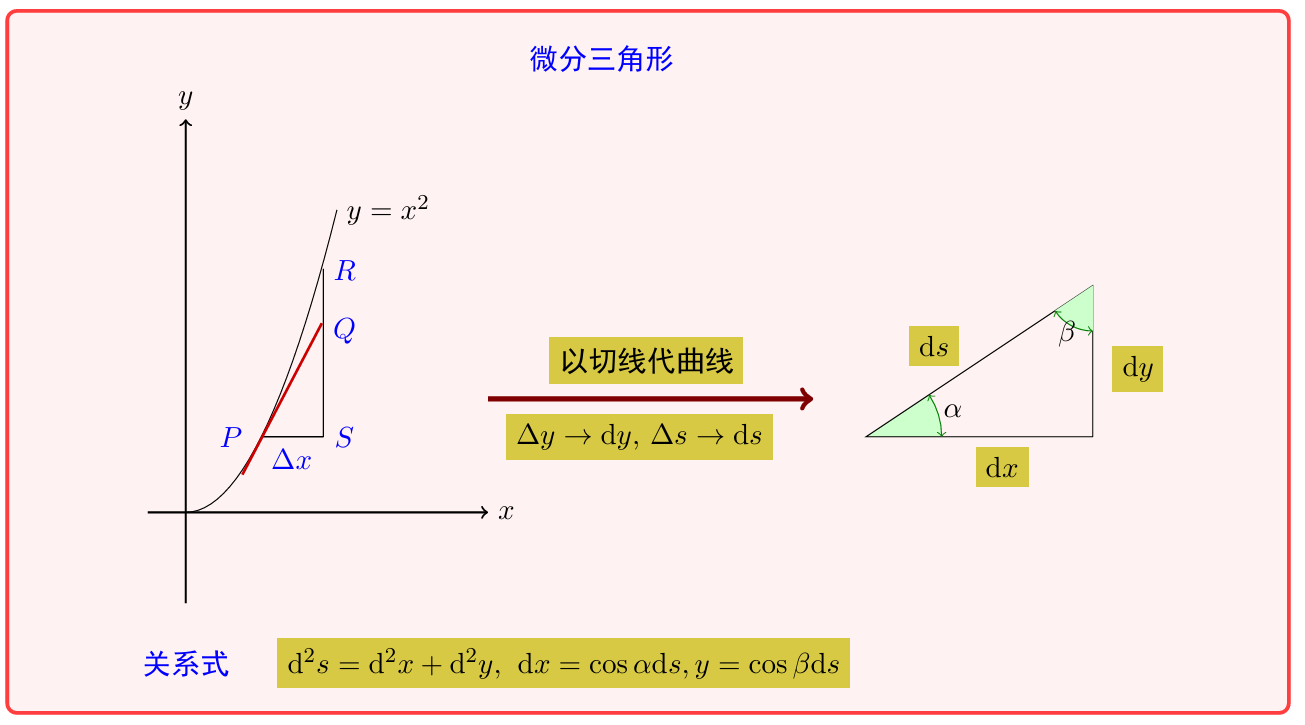
以直代曲. 曲线用切线近似
在微分三角形中可以得到切线的夹角, 斜率, 弧微分\(ds\)(斜边)之间的关系.
\[ \begin{align} \frac{dy}{dx}&=\tan \alpha,\\ d^2 s&=d^2 x+d^2 y,\\ d s&=\sqrt{1+y'^2}\ d x,\\ d x&=\cos\alpha d s, y=\cos\beta d s. \end{align}\]
4 常见函数的导数
- 几个基本初等函数的导数
\[ \begin{align} (x^\alpha)'=\alpha x^{\alpha-1},\\ (a^x)'=a^x\ln a,\\ (\log_a x)'=\frac{1}{x\ln a},\\ (\sin x)'=-\cos x,\\ (\cos x)'=\sin x,\\ (\tan x)'=\sec^2 x,\\ (\cot x)'=-\csc^2 x,\\ (\sec x)'=\sec^2 x\tan x,\\ (\csc x)'=-\csc^2 x\cot x,\\ (\arctan x)'=\frac{1}{1+x^2},\\ (\arcsin x)'=\frac{1}{\sqrt{1-x^2}}.\\ \end{align} \]
5 高阶导数
高阶导数就是导数的导数, 所以前面的求导方法都可以使用.
不过是符号, 计算过程复杂一些.
- 可以用函数的幂级数展开式求高阶导数.
设\(y=f(x)\) 则 \[ y^{(n)}=(y^{(n-1)})'=\frac{d^n y}{d x^n}=\frac{d^n f}{d x^n}=\frac{d^n }{d x^n}f(x). \]
\[ (uv)^{(n)}=\sum_{i=0}^n C_n^i u^{(n-i)}v^{(i)}. \]
- 求和项和二项式展开式类似.
定理 如果函数在\([a, b)\)上可微, 右连续. 导数\(f'(x)\)在点\(a\)存在右极限\(f'(a+0)=A.\) 则\(f(x)\)也一定存在右侧导数\(f'_+(a),\) 且 \[f'(a+0)=f'_+(a)=A.\]
- 如果函数处处有导数, 则导数或者连续或者是第二类间断点(左极限, 右极限至少一个不存在)
- 明白概念定义
导数\(f'(x)\)的右极限 \[f'(a+0)=A=\lim_{x\rightarrow a^+}f'(x).\]
右侧导数 \[f'_+(a)=\lim_{x\rightarrow a^+}\frac{f(x)-f(a)}{x-a}\]
对右侧导数用拉格朗日中值定理即证.
\[f'_+(a)=\lim_{x\rightarrow a^+}\frac{f(x)-f(a)}{x-a}=\lim_{x\rightarrow a^+}f'(\xi)=A.\]
- Darboux定理 函数在区间上可导, 则导数有介值性.
设\(f'(a)<c<f'(b).\)
构造函数 \[ F(x)=f(x)-cx, \]
最小值点即为答案.
注意要讨论最小值点在不在端点.
6 用导数
- 符号决定一切
- 导(函)数的符号决定单调性;
- 二阶导(函)数的符号决定凹凸性;
- 一点处二阶导数的符号决定是极大极小.
- 变号决定一切
- 导数左右变号的点是极值点;
- 二阶导数左右变号的点是拐点.
导(函)数的符号决定单调性.
极值的必要条件: 一阶导数为0
极值的充分条件: 一阶导数为0, 二阶导数不等于0.
极大还是极小用例子\(y=x^2\)或泰勒公式帮助记忆 \[ f(x)-f(x_0)= \frac{f''(\xi)}{2}(x-x_0)^2. \]
求极值的步骤
找出可能的点(驻点, 导数不存在的点), 判断是不是.
实际问题如果函数只有一个驻点, 一般是极值点.
二阶导(函)数的符号决定凹凸性
凹函数的意义(记住例子\(y=x^2\)) \[\frac{f(x_1)+f(x_2)}{2}\geq f(\frac{x_1+x_2}{2}).\] 反过来也可以用二阶导数判断凹凸性, 然后证明这个不等式.
曲线在割线的下面
曲线在切线的上面
切线的斜率单调增加
二阶导数大于0.
\(y=kx+b\)是\(y=f(x)\)的斜渐近线, 就是当\(x\rightarrow \infty\)时, 两条曲线上的点靠得越来越近, 即 \[ \lim_{x\rightarrow +\infty}f(x)-(kx+b)=0. \] 所以 \[ k=\lim_{x\rightarrow +\infty} \frac{f(x)}{x}. \] 求得斜率, 再代入上一个极限式子中求\(b.\)
渐近线有3类: 水平, 铅直, 斜.
- 公式.
- 运用表格使得过程简洁明了.
7 题目
设\(f(x)\)在\(x=0\)处可导, 且\(f(0)=f'(0)=2,\) 求 \[\begin{align} &\lim_{n \rightarrow \infty}\left(\frac{f(\frac{2}{n})}{f(0)} \right)^n. \end{align}\]
条件是一点处可导, 用一点处导数的定义.
指数形式, 重要极限.
方法是凑出导数的定义的形式
计算:
\[\begin{align} &\lim_{n \rightarrow \infty}\left(\frac{f(\frac{2}{n})}{f(0)} \right)^n\\ =&\lim_{n \rightarrow \infty}\left(1+\frac{f(\frac{2}{n})-f(0)}{f(0)} \right)^n\\ =&\lim_{n \rightarrow \infty}\left(1+\frac{f(\frac{2}{n})-f(0)}{f(0)} \right)^{\frac{f(0)}{f(\frac{2}{n})-f(0)} \cdot \frac{f(\frac{2}{n})-f(0)}{\frac{2}{n}}}\\ =&e^{f'(0)}. \end{align} \]
用指数函数简化以下过程. \[\begin{align} &\lim_{n \rightarrow \infty}\left(\frac{f(\frac{2}{n})}{f(0)} \right)^n\\ =&\lim_{n \rightarrow \infty} e^{n\ln\left(1+\frac{f(\frac{2}{n})-f(0)}{f(0)} \right)}\\ =&\lim_{n \rightarrow \infty} e^{n \frac{f(\frac{2}{n})-f(0)}{f(0)} }\\ =&\lim_{n \rightarrow \infty} e^\frac{f(\frac{2}{n})-f(0)}{\frac{2}{n}}\\ =&e^{f'(0)}. \end{align} \]