函数
\[y=f(x)\]
- 函数就是映射, 由对应法则和定义域决定.
- 对应法则可以用各种各样的方式告诉我们.
- 不管函数怎样表示, 我们关注的都是它如何变化? 有什么性质? 各种方式表示的函数的导数或微分怎么求?
- 研究函数的工具方法都相同: 导数, 微分, 积分. 只不过不同表达式计算导数时方法不一样.
1 函数是什么?
- 定义域.
- 对应法则.
2 函数的表达方式
- 函数有各种各样的表达方式.
- 目的都是为了更好的描述函数或不得已而为之.
- 不管哪种表达方式, 最基本的问题是搞清楚研究对象: 谁是自变量? 谁是因变量
- 如果是很奇怪的表达方式, 先要确定是不是一个函数.
直接写出来,
例如, 一元函数 \(y=x^2,\) 二元函数 \(z=xy-\ln(x+y)\).
- 没有统一的表达式—-没办法. \[ y=\left\{\begin{array}{ll} 1,& x\mbox{是有理数}, \\ 0,& x\mbox{是无理数}. \end{array} \right. \]
- 只知道变量之间有关系, 但不容易写出直接的解析关系或根本就写不出来. \[ \sin x e^y=xy+2. \]
要明白确定了几个函数, 谁是自变量, 因变量? \[ \left\{\begin{array}{ll} x+y+z=2, \\ 3x+y-4z=2. \end{array} \right. \]
3个未知数, 2个方程, 可以解出两个未知数.
所以有一个是自变量, 另外两个可以解出来. 如
\[ \left\{\begin{array}{ll} y=f(x), \\ z=g(x). \end{array} \right. \]
- 实际上也可以看成参数方程.
\[ \left\{\begin{array}{ll} x=a\cos t , \\ y=b\sin t. \end{array} \right. \]
- 有了参数\(t\)就可以把看起来不相关的变量\(x,y\)联系起来了.
- 注意有时\(x,y\)的直接联系可能很复杂.
- 参数方程会使函数表示得较为简单.
谁是自变量, 谁是因变量不好说? 一个等式中的两个字母都有可能, 要根据需要确定. 比如 \[x+y+1=0.\]
可以得到\(y=1-x\),
也能得到\(x=1-y.\)
\(y=f(u), u=\phi(x).\)
出现了中间变量\(u\), 如图: \[ y\xrightarrow[]{f(u)}u \xrightarrow[]{\phi(x)}x \]
复合函数本质是用两个已知函数来构造一个新的函数.
\[\int_a^x e^{t^2}dt.\]
实际问题中会要求积分的上下限变化.
实际上是一个函数.
这个函数的导数很容易得到.
- 函数本身不知道是什么, 但函数和导数满足某些关系.
- 比如弹簧随时间的位移变化, 知道每个时刻的变化率(速度)的变化率(加速度), 可以由此列出微分方程, 由导数来确定函数关系. 如 \[y'=2x, y(0)=0.\]
\[ 1+x+x^2+\cdots .\]
无限和, 需要先确定是不是函数? 即收敛域, 不收敛则没有意义, 不是函数.
很多时候需要这种表达式, 而且有时用这种表达式解决问题更容易.
3 初等函数
基本初等函数要清楚, 这是基础.
初等函数是由基本初等函数构造的.
4 例题分析
下面这两个无限和是不是函数? \[\begin{aligned} f(x)&=1+x+x^2+x^3+\cdots;\\ g(x)&=1+x+2!x^2+3!x^3+\cdots. \end{aligned}\]
是不是函数就看对于一个\(x\), 是否有唯一的\(y\)与之对应.
下面表示的是什么函数? 其中字母都表示未知数. \[\begin{aligned} 1.&\ x^y=y^x.\\ 2.& \left\{\begin{array}{l} x^y-yz=z^x-1\\ y^z+xz=x^2+2 \end{array} \right..\\ 3.& \left\{\begin{array}{l} 4xy-3yz=ze^x-wy\\ 2^z+xwz=x^2+2y \end{array} \right.. \end{aligned} \]
- 理论上说一个方程可以解出一个未知数, 两个方程组成的方程组可以解出两个未知数.
- 如果两个方程的方程组有3个未知数, 那就先给定一个未知数的值,比如\(x\), 就可以解出剩余两个未知量的值\(y, z,\) 从而同时 得到两个一元函数\(y=y(z), z=z(x).\)
- 方程组如有4个未知数, 先给定两个未知数的值, 可以解出剩余两个未知量, 就同时得到两个二元函数.
- 哪些字母作为自变量, 没有限制, 要根据题目要求决定.
5 问与答
能够把幂函数, 指数函数, 对数函数, 三角函数, 反三角函数的图形画出来吗?
试一试! 这是一切函数的基础.
6 如何研究一元函数?
6.1 让函数变化
如 \(y=f(x)\), 让自变量增加\(\Delta x,\) 看看 \[\Delta y=f(x+\Delta x)-f(x)\] 如何变化.
实际上, 我们大部分的时间都在研究, 估计 \(\Delta y\).
6.2 不断近似, 逼近\(\Delta y\)
- \(\Delta y\)一般很复杂, 我们先简单地近似, 如误差太大, 再想法减少误差, 逐步达到要求.
6.3 第一步, 连续
\[ \lim_{\Delta x\rightarrow 0}\Delta y=0. \]
得到定性的结果, \(\Delta y\)是一个无穷小.
到底多小, 没有数量的估计.
6.4 第二步, 可导
\[ \lim_{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=f'(x)=\frac{d y}{d x}. \]
定量估计: \[ {\Delta y}\approx f'(x)\Delta x=d y. \]
准确描述一: \[ {\Delta y}= f'(x)\Delta x+o(\Delta x) . \]
准确描述二: \[ {\Delta y}= f'(\xi)\Delta x . \]
6.5 第三步, 泰勒公式
如果对误差还不满意, 再逼近一点, 可以进一步用高阶导数描述近似值, 误差更小, 就得到泰勒公式了.
注意 实际问题中, 准确得到\(\Delta y\) 一般没有必要, 也不可行, 我们只需得到一个满足误差要求的近似值就行.
6.6 几何解释
以直代曲. 曲线用切线近似.
微分三角形
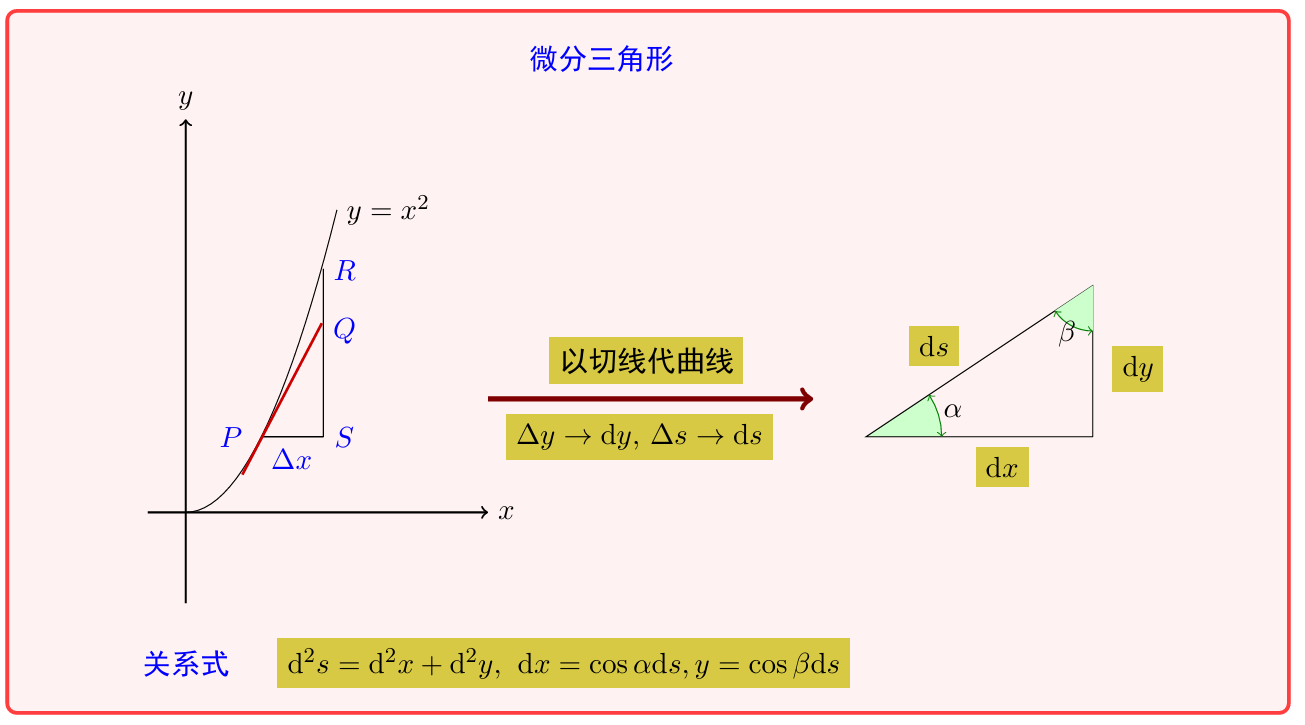
- 牢记研究函数的目标: 近似+控制误差.